<【配资平台开户炒股】>深入探讨频率与波长的数学关系及在不同领域的应用

引言

波动现象是自然界最普遍的存在形式之一波长 频率，从光波传递能量到声波传递信息深入探讨频率与波长的数学关系及在不同领域的应用，从无线电通信到医学成像，频率（ff）与波长（λλ）的关系始终是理解这些现象的核心。本文将从基础物理学出发，深入探讨二者的数学关系及其在不同领域的实际应用。

一、基本概念与数学关系

1. 定义与单位

· 波长：相邻波峰或波谷之间的空间距离，单位为米（m）。例如可见光的波长在380-780纳米之间。

· 频率：单位时间内通过某点的完整波动周期数，单位为赫兹（Hz）。人耳可感知的声波频率范围为20-20000 Hz。

· 波速（vv）：波在介质中传播的速度，真空中光速为3×108 m/s3×108m/s。

2. 反比关系的数学表达

三者满足基本方程：

v=fλv=fλ

当波速固定时（如真空中的光速），频率与波长严格成反比：

f∝1λf∝λ1

这一关系适用于所有波动类型，包括电磁波、声波和水波。

二、不同类型波动的特性对比

1. 光波：颜色与能量的载体

· 可见光谱：红光（长波长，~700 nm，低频）到紫光（短波长，~400 nm，高频）的渐变对应颜色变化。

· 能量计算：以500 nm绿光为例，其频率为：

f=cλ=3××10−9=6×1014 Hzf=λc=500×10−93×108=6×

波长缩短至400 nm时，频率升至7.5×1014 Hz7.5×，能量更高。

2. 声波：音调与传播特性

· 低音提琴的基频约40 Hz（波长8.5米），而小提琴高音弦达3000 Hz（波长仅0.11米）。

· 超声波的频率超过20 kHz，短波长特性使其可用于微观成像（如B超分辨率达毫米级）。

三、电磁波谱的工程化应用

1. 通信技术

· 无线电波：调频广播（88-108 MHz，波长3-2.7米）利用长波长绕射特性实现远距离传播。

· 微波：2.4 GHz WiFi信号波长12.5厘米，可穿透墙体但易被金属屏蔽。

· 光纤通信：1550 nm红外光（频率193 THz）在石英光纤中传输损耗最低，支撑全球互联网骨干网。

2. 工业与科研

· 紫外光刻：248 nm深紫外光（DUV）在芯片制造中实现90 nm线宽，而13.5 nm极紫外光（EUV）突破5 nm制程。

· 雷达系统：X波段（8-12 GHz，波长3.75-2.5 cm）用于气象雷达，而L波段（1-2 GHz）适合远程航空管制。

四、介质影响与特殊场景

1. 波速变化的效应

在非真空介质中，频率保持不变，但波速降低导致波长缩短。例如：

· 水中光速降至真空的75%，红光（空气中650 nm）波长变为487.5 nm。

· 声波在钢中的传播速度达5100 m/s，是空气中的15倍，波长相应延长。

2. 非线性关系特例

某些复杂系统中，波长与频率可能呈现非线性关系。例如：

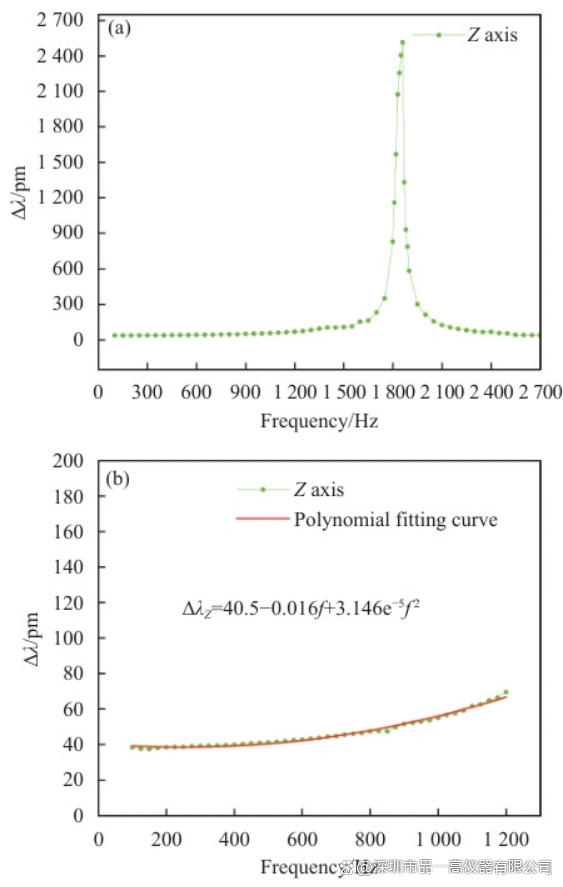
· 光纤布拉格光栅（FBG）传感器在1200 Hz以上高频激励时，波长变化Δλ与频率ff满足：

Δλ=40.5−0.016f+3.146×10−5f2Δλ=40.5−0.016f+3.146×10−5f2

这反映了材料共振带来的特殊响应。

五、测量方法与技术演进

1. 经典测量工具

· 光栅光谱仪：通过衍射条纹间距计算波长，精度达0.01 nm。

· 驻波法测声速：调节空气柱长度产生共振，利用λ=2L/nλ=2L/n计算波长。

2. 现代技术突破

· 飞秒光频梳：通过锁定激光频率，实现波长测量不确定度小于1×10−181×10−18。

· 量子传感器：基于里德伯原子的电磁场探测，可同时解析频率与波长参数。

六、跨学科应用案例

1. 环境监测

· 多普勒气象雷达通过回波频率变化（±10^3 Hz）反演降水粒子运动速度。

· 海洋浮标使用1-5 Hz次声波监测海啸，波长数百公里的特性适合大范围追踪。

2. 生物医学

· 光学相干断层扫描（OCT）利用1300 nm近红外光（低频）穿透生物组织，分辨率达微米级。

· 质子治疗中，束流频率调谐至肿瘤组织共振频率，实现能量精准沉积。

结语

频率与波长的反比关系不仅是教科书中的基础公式，更是驱动现代科技发展的核心原理。从5G通信的毫米波设计到引力波探测的激光干涉，从量子计算的微波控制到深空探测的射电望远镜，对这一关系的深入理解持续推动着人类认知边界的拓展。随着超材料、拓扑光子学等新兴领域的发展，频率与波长的调控将开启更多前所未有的应用场景。

作者声明：作品含AI生成内容